对很多人来说，数学是一门很难学的学科，它十分普遍，在许多领域都有各种各样的应用。线性代数是数学的一部分，理解和应用起来尤其困难。在我看来，关于线性代数的许多课程和开源工具都需要大量的计算。对于刚接触线代的新人来说，这可能是个问题。线性代数在数据科学和机器学习中有各种各样的应用——举几个例子：自然语言处理、推荐系统、降维、神经网络等。对线性代数有较强的基础理解将有利于理解机器学习的底层逻辑和数学方法。

  本文将着重于通过图形的使用来从视觉上理解线性代数的计算，这将涵盖许多核心概念，如矩阵的加法、减法、乘法、除法、转置等。这些是线性代数中非常基本和常见的概念，这些概念在机器学习中也经常出现。

  图论和线性代数是相辅相成的，数学中有一个完整的子范畴叫作代数图论，它使用代数方法来解决有关图的问题。这些代数方法往往包括各种线性代数。

  本文使用的核心概念是邻接矩阵。邻接矩阵是指可以将一个图G转换成一个矩阵，反之亦然。邻接矩阵总是对称的，由表示图G中相邻顶点对之间连接的元素组成。图到相关邻接矩阵的转换可以很容易地在下面的图中说明。

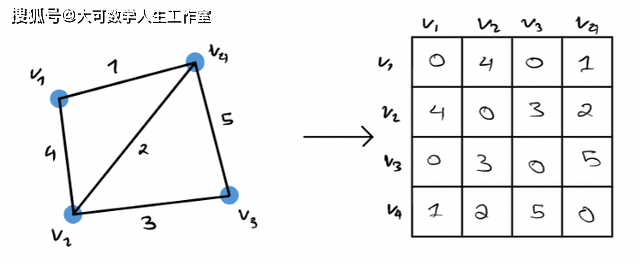
  如果图G有任何自循环，在上图中矩阵的对角线上就会有值。邻接矩阵封装了图的结构和关系。邻接矩阵可以表示为稀疏或密集矩阵，使其在图上运行实验的计算效率非常高。因此，邻接矩阵是表示图的最常用方法之一。在本文中，我将把线性代数中介绍的基本概念应用到邻接矩阵中，并展示与该矩阵相关联的图是如何相应地变化的。

  对大多数人来说，对矩阵进行算术运算是格外的简单和直观的。理解基于算法的图最简单的方法是通过加权图。通过线性代数中涉及的一般算术，与这些算术相关的图形可能会发生巨大的变化。新的边能形成或移除，与这些边相关的影响将增加或减少重要性。这个图可以从一个连通的网络变成一个不连通的网络。下面展示的示例可以更好地从视觉上理解图上的矩阵算术。

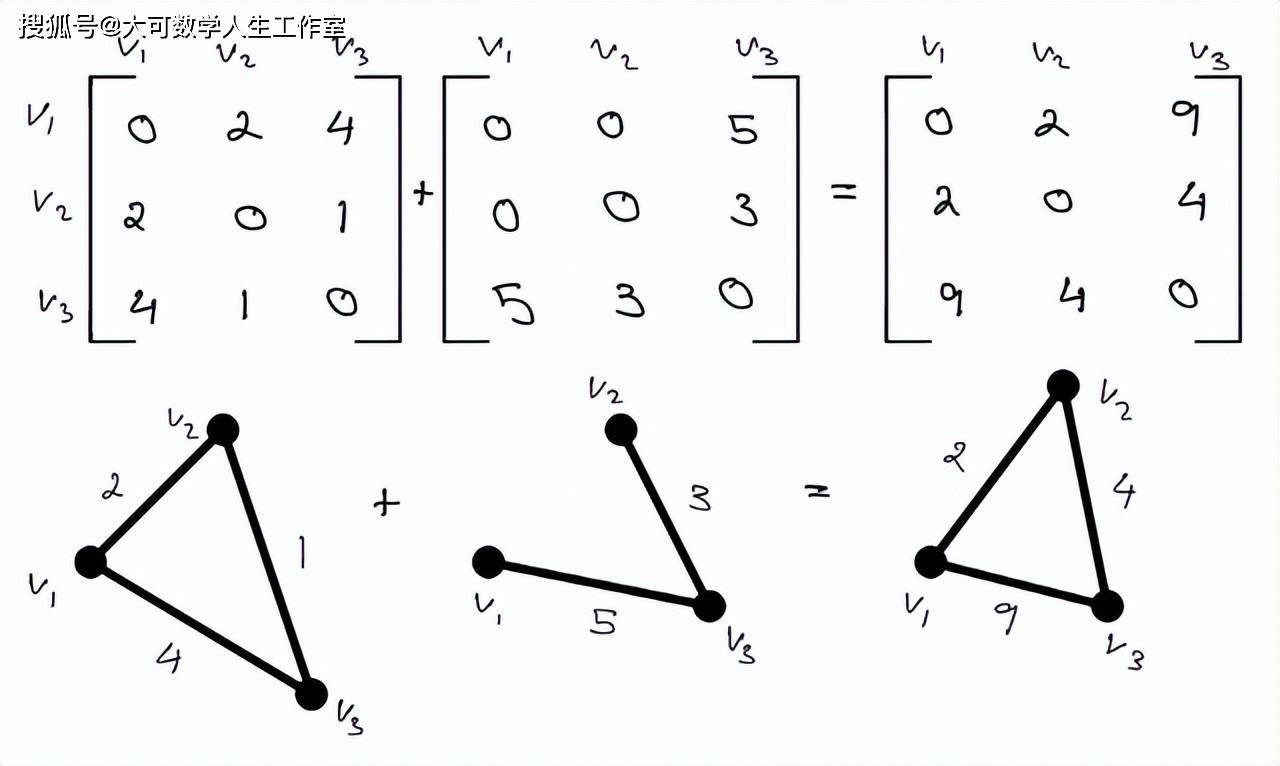
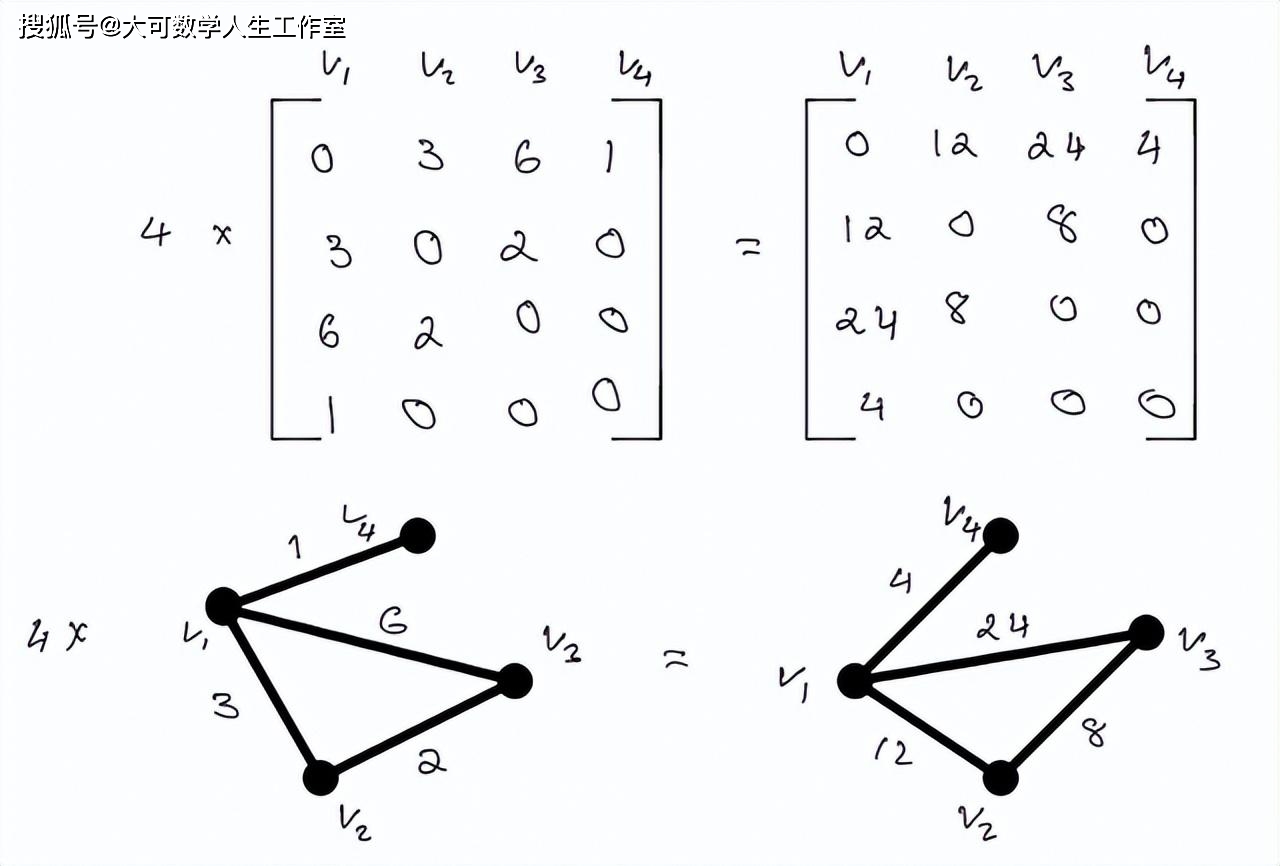
  点积是一个很难从视觉上理解的概念，特别是当你要相乘的矩阵的维数很大的时候。当研究如下所示的图像时，请记住，当取两个图的点积时，它几乎肯定会成为一个有向图。下图你将看到取两个无向图（邻接矩阵）的点积的结果，它是有向图。在最简单的形式中，如果一个图不包含重复边和循环，它就是无向图。这在某种程度上预示着无向图的邻接矩阵对角线为零，且矩阵M^T的转置等价于M。

  正如你将看到的，有向图是非常不同的。有向图是由有向边组成的图，这在某种程度上预示着只有在有向边到达某个节点时才能从一个节点到另一个节点。方向通常通过边上的箭头来指示。

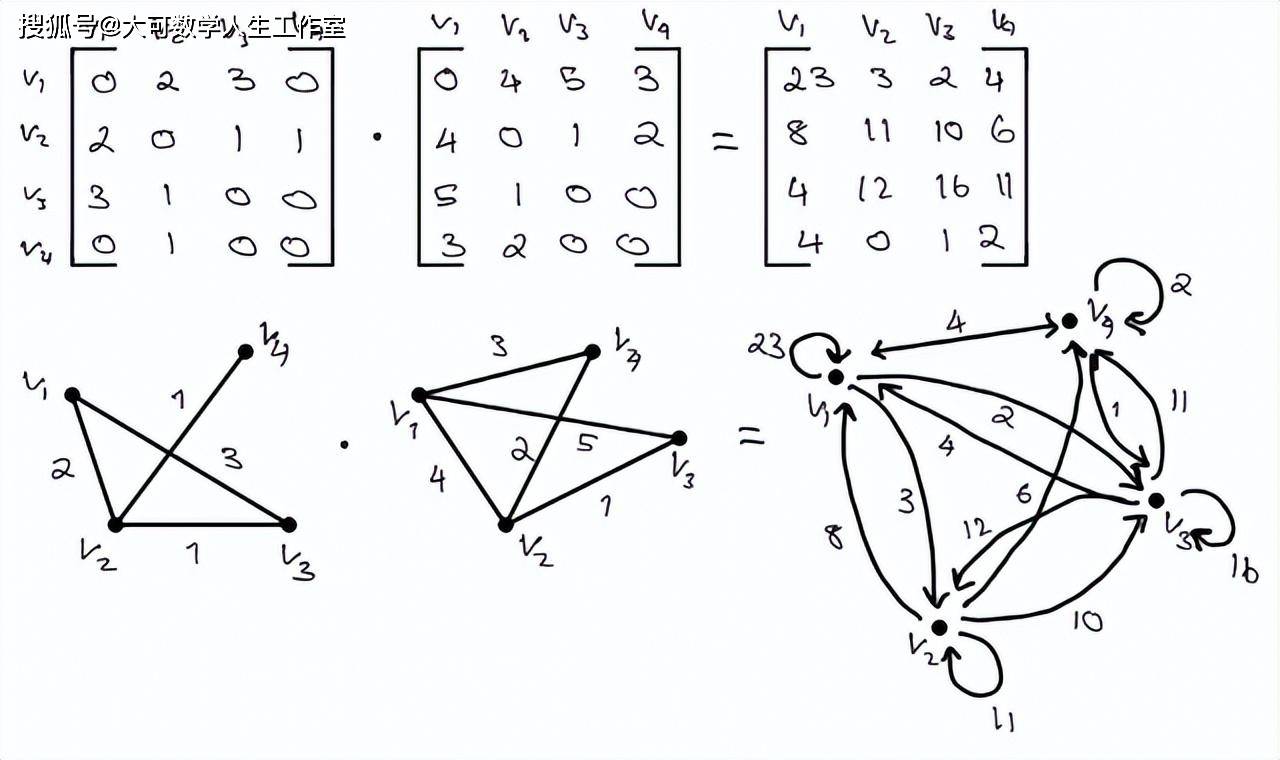
  点积得到的图完全改变了人们对图的理解。两个（相对）简单图的点积会导致一些相当混乱的结果。正如你所看到的，你可以遍历具有不一样权值的各个节点。

  传统上，当我们要转置一个矩阵时，所要做的就是在它的对角线上翻转这个矩阵。但是这怎么样影响相关的图呢？

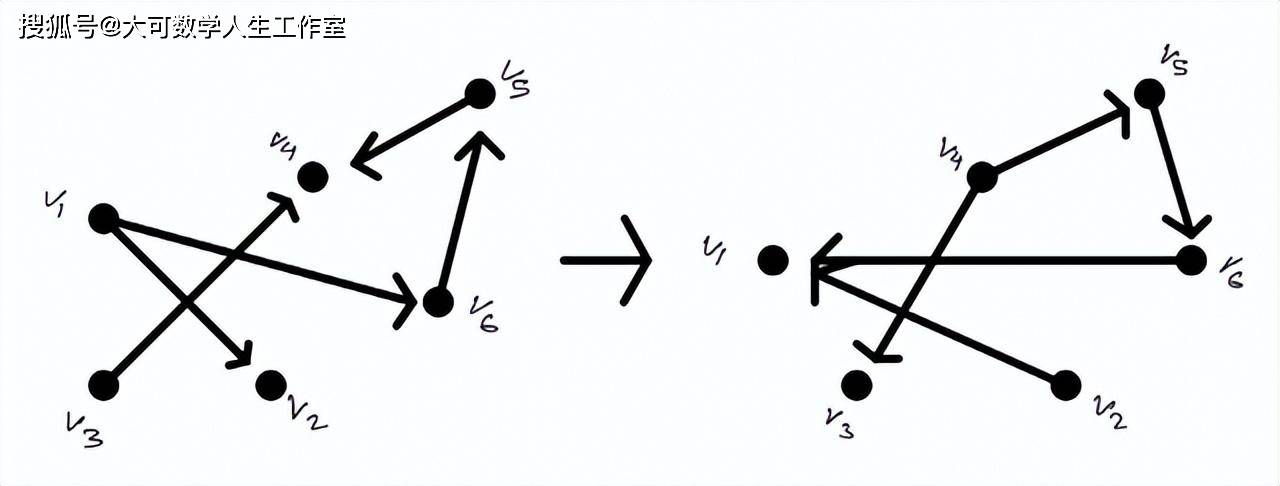
  转置背后最简单的视觉理解是通过观察有向图。如上所述，当图G的一个节点通过一条边指向另一个节点时，图G是有方向的，那么该图G的转置将表明方向被交换了。这可能是对矩阵转置怎么样影响网络的最直观的理解。

  由一组项和常数组成的表达式。这个表达式是每一项乘以它的相关常数的乘积的和。可以用以下公式数学表示：

  现在，当在图的背景下考虑线性组合时，假设每个向量现在是一个对应于图的对称矩阵。然后，我们大家可以直观地看到，当合并网络时，每个变化所产生的影响。如下图所示：

  线性代数在机器学习中的应用有很多种。独热编码、多种降维模型等概念从根本上起源于线性代数。像PCA这样的模型直观地使用了线性组合和特征向量背后的思想，以减少输入数据，同时最好能够降低信息丢失。

  线性代数在机器学习中的更复杂应用表现为推荐系统和深度学习。所有形式的推荐系统都使用各种线性代数来解决所提出的问题。基于内容、协同过滤和混合方法解决推荐系统中的问题，使用线性代数中的常见概念，如点积、余弦相似度、欧几里德距离、矩阵分解等。在推荐系统中，即使是像链接预测这样的复杂方法，也从根本上使用大量的线性代数来识别网络中缺失的边。

  深度学习的本质是线性代数，从用于定义神经网络的数据结构到它在训练和测试数据中的方法。深度学习中一个常见的术语是张量，张量本质上是一个超过二维的矩阵。

  我希望这篇文章能为你提供图论和线性代数数学背后的直觉和联系。这些概念常常会出现在各种机器学习和数据科学应用的幕后。对这些概念有一个更严格和基础的理解，将最大有可能帮助你学习各种机器学习相关的概念。返回搜狐，查看更加多