本文将讨论我们大家常常遇到的概率分布，希望能从概念层面帮大家建立总体认知。

  在平时的科研中，我们大家常常使用统计概率的相关知识来让我们进行城市研究。因此，掌握一定的统计概率相关知识非常有必要。

  如果实验可能的结果是可数的，那么它被称为离散随机变量。例如，如果你抛硬币 10 次，你能得到的正面数可以用一个数字表示。或者篮子里有多少苹果仍然是可数的。

  这些是不能以离散方式表示的值。例如，一个人可能有 1.7 米高，1米 80 厘米，1.6666666...米高等等。

  返回离散随机变量 等于 的值的概率。所有值的总和等于 1。PMF 只能用于离散变量。

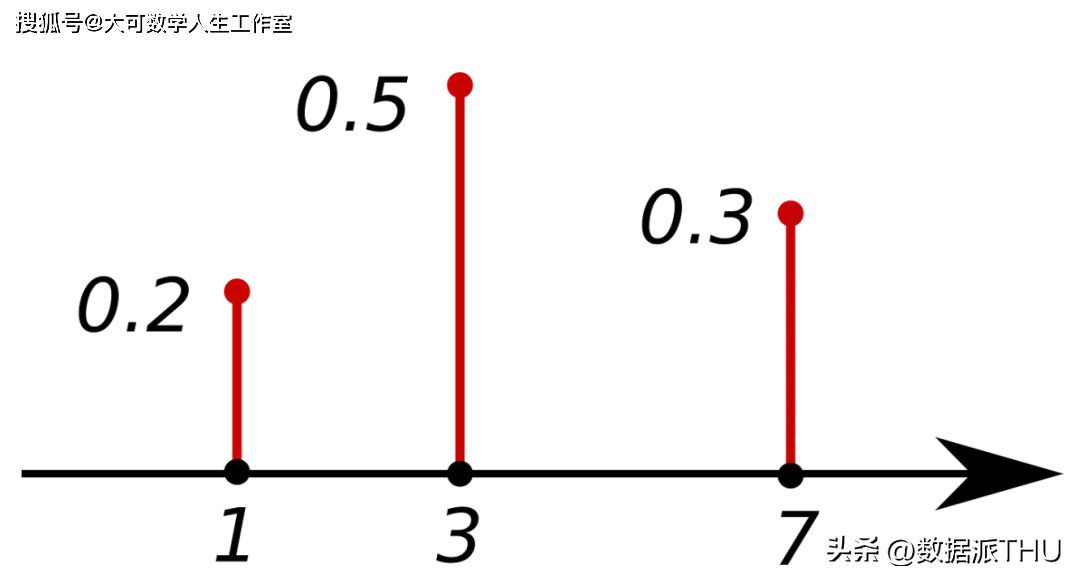
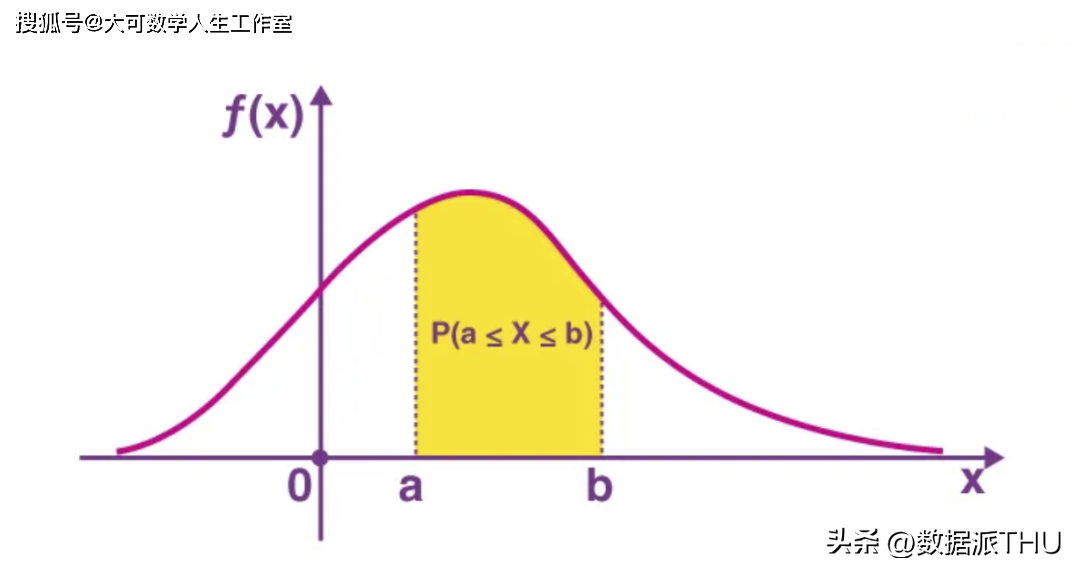
  它类似于连续变量的 PMF 版本。返回连续随机变量 X 在某个范围内的概率。

  我们有一个线)的结果。假设我们接受正面为真（我们大家可以选择正面为真或成功）。那么，如果正面朝上的概率是 ，相反情况的概率就是 。

  伯努利分布是针对单个观测结果的。多个伯努利观测结果会产生二项式分布。例如，连续抛掷硬币。

  现在这次，你有一枚欺诈硬币。你了解这一个硬币正面向上的概率是 0.7。因此，p = 0.7。

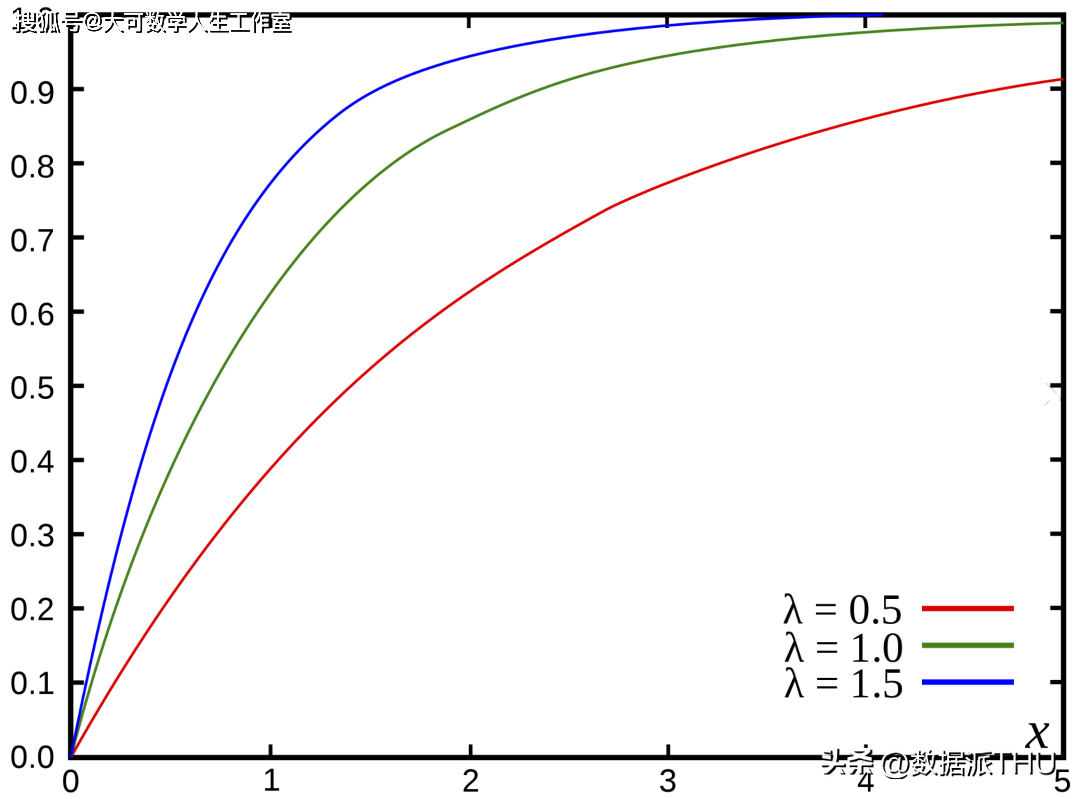
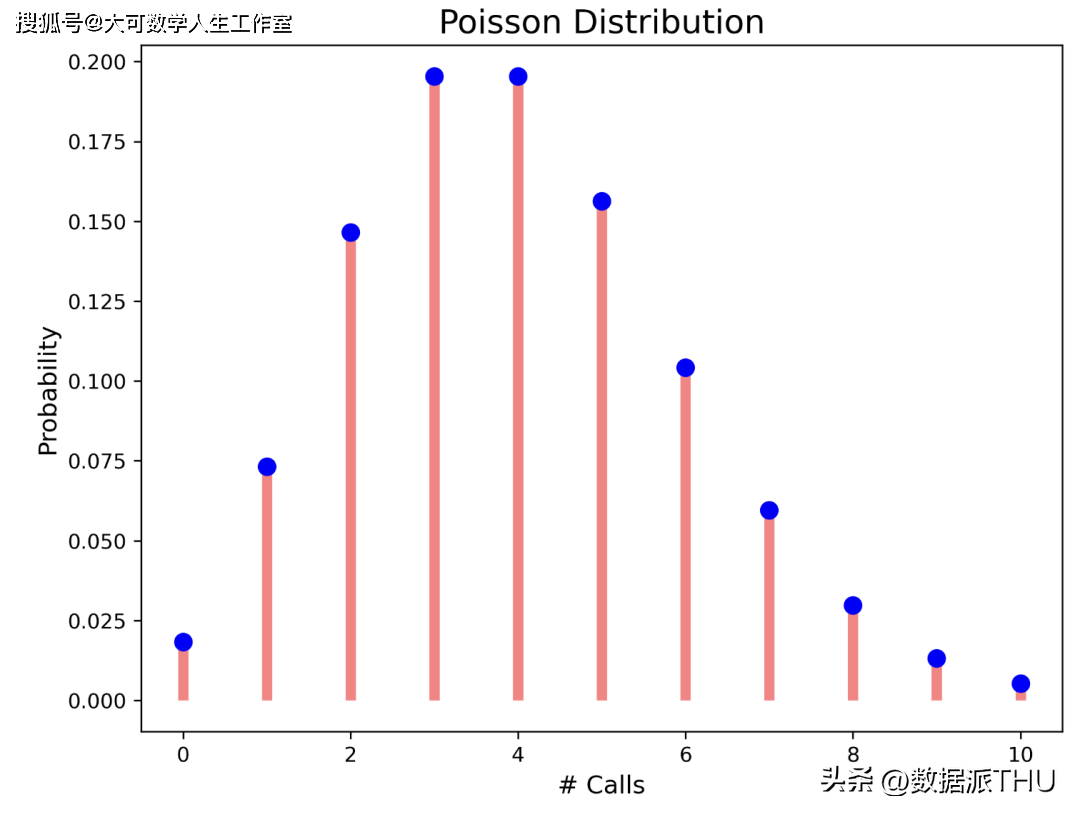
  ， 是在指定时间间隔内预期发生的事件次数。它是在该时间间隔内发生的事件的已知平均值。 是事件在指定时间间隔内发生的次数。如果事件遵循泊松分布，则：

  在泊松分布中，事件彼此独立。事件可以发生任意次数。两个事件不能同时发生。

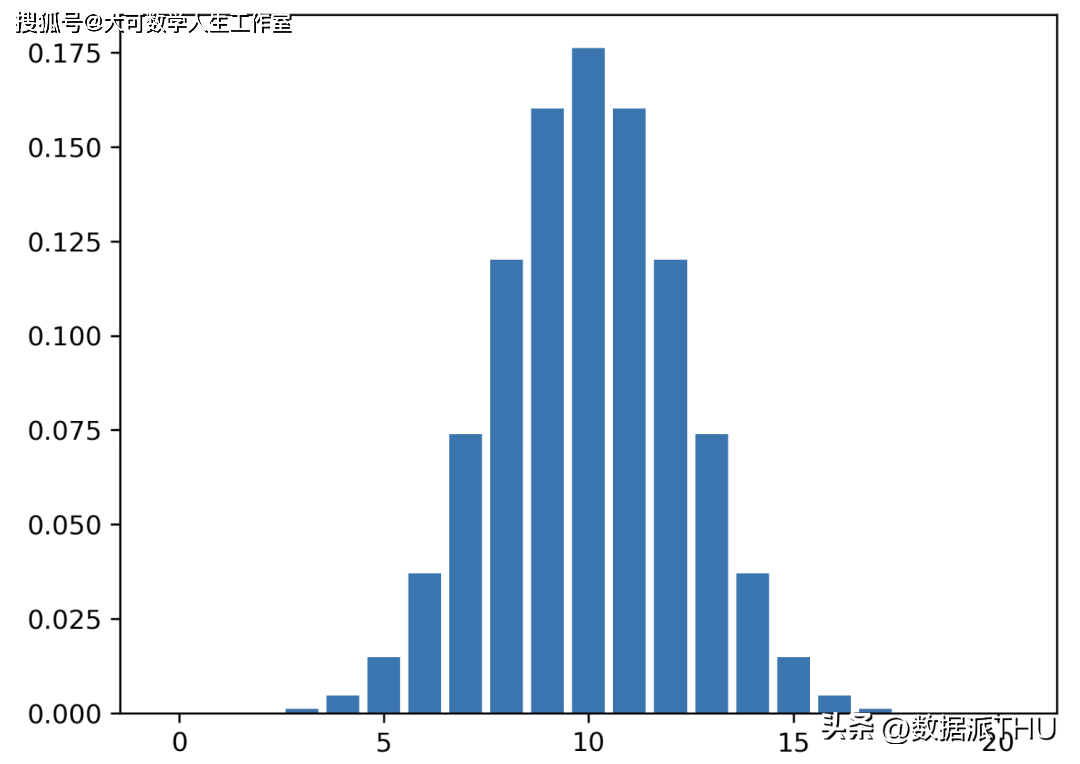
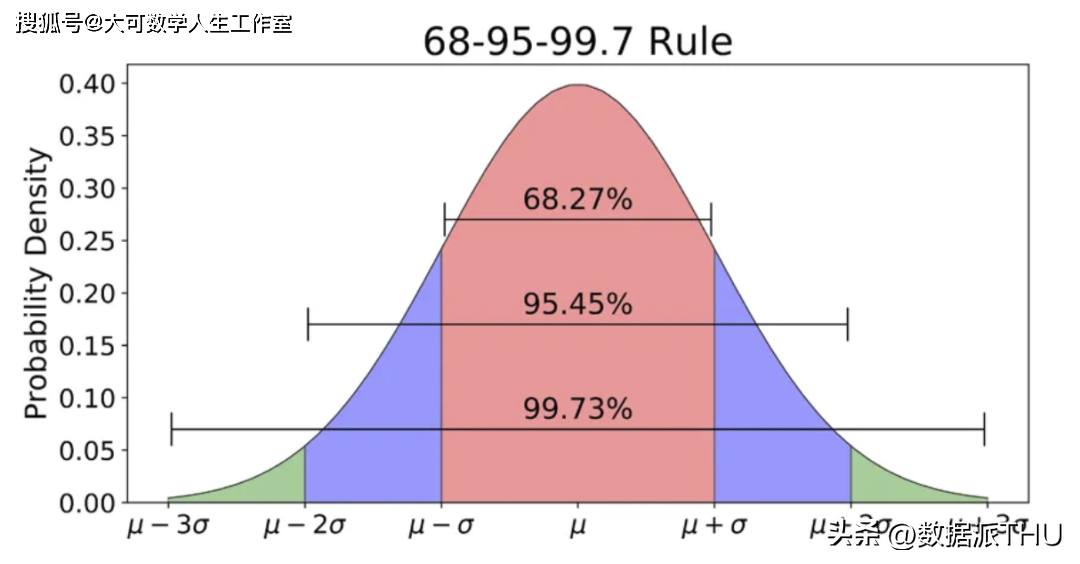
  最著名和最常见的分布（也称为高斯分布），是一种钟形曲线。它能够最终靠均值和标准差定义。正态分布的期望值是均值。

  曲线对称。均值、中位数和众数相等。曲线%的值落在一个标准差范围内。~95% 落在两个标准差范围内，~98.7% 落在三个标准差范围内。

  计算每个数据点的 z 分数并对其进行排序，然后在 y 轴上表示它们。X 轴表示值的排名的分位数。

  generate_skew_data(1000, 100, 5) # positive (5)- 右偏分布

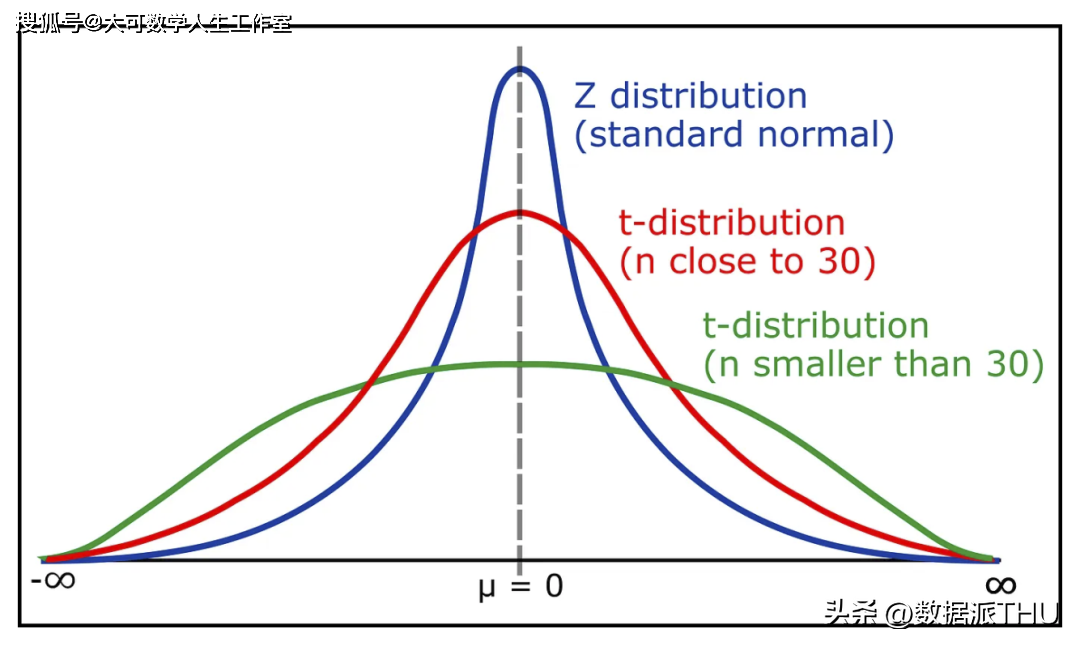
  t 分布是具有较厚尾部的正态分布。如果可用数据较少（约 30 个），则使用 t 分布代替正态分布。

  在 t 分布中，自由度变量也被考虑在内。根据自由度和置信水平在 t 分布表中找到关键的 t 值。这些值用于假设检验。

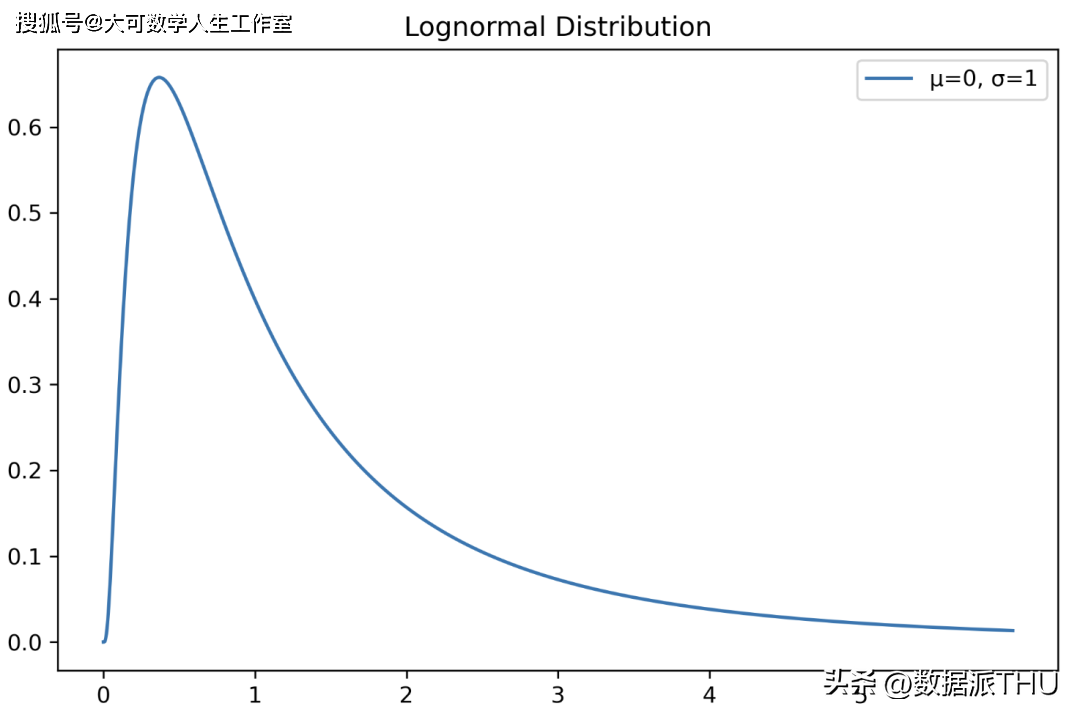
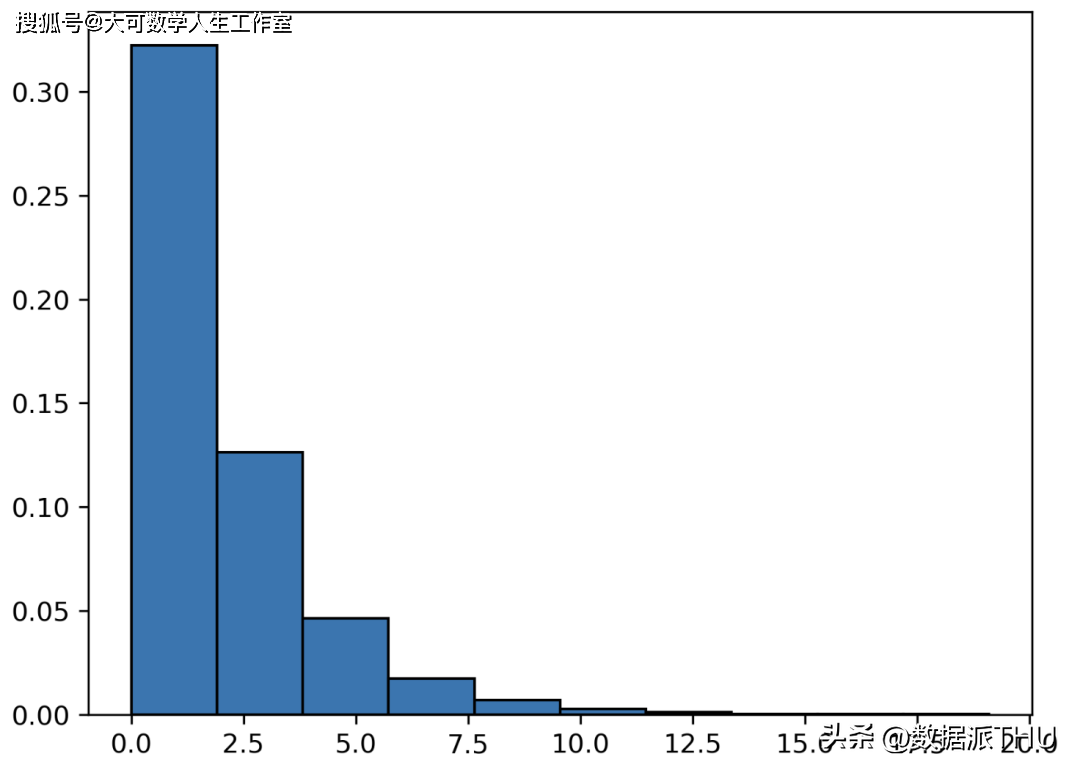
  它是指时间间隔是可变的而不是固定的情况下使用的指数分布的扩展。在 Weibull 分布中，时间间隔被允许动态变化。

  是形状参数，如果是正值，则事件发生的概率随时间而增加，反之亦然。 是尺度参数。

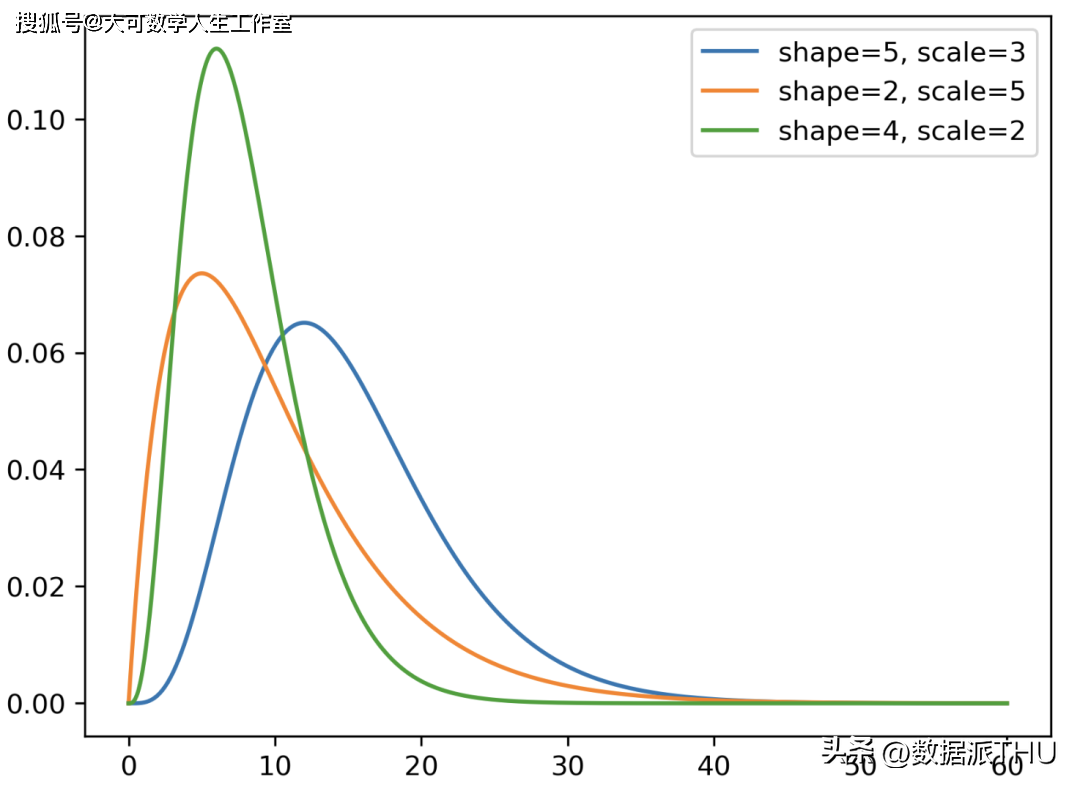
  Gamma 分布。X 轴表示随机变量 X 可能取到的潜在值，Y 轴表示分布的概率密度函数（PDF）值

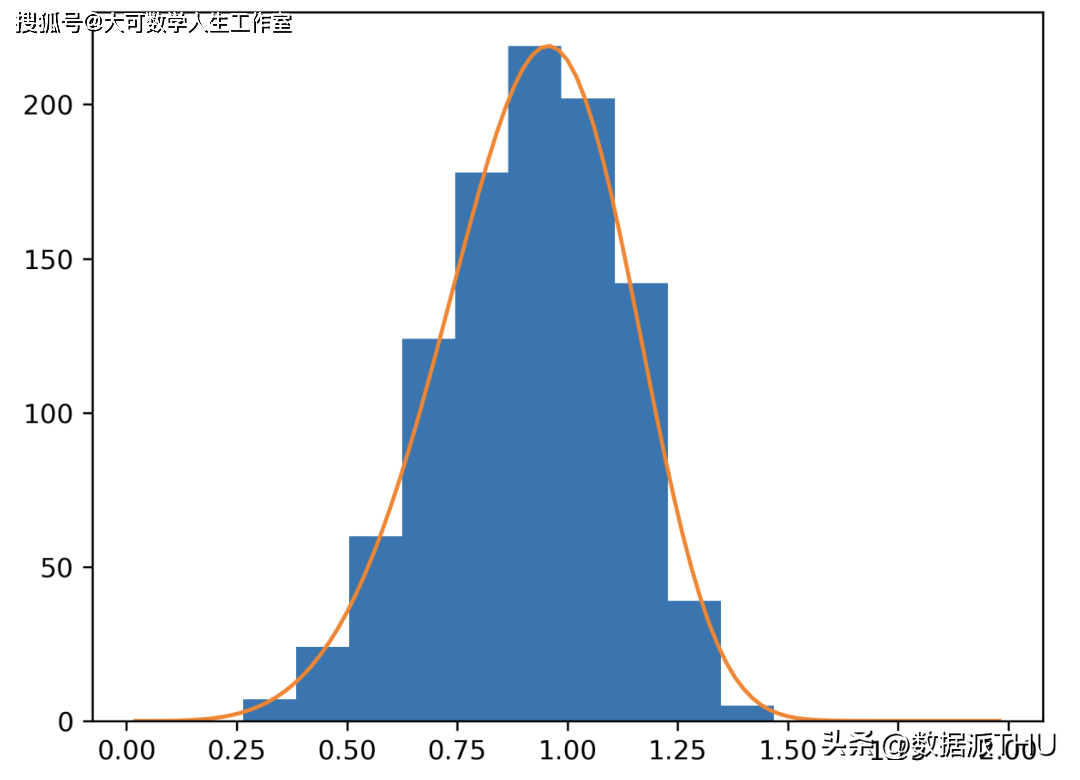
  我们可以从任何分布（离散或连续）开始，从人群中收集样本并记录这些样本的平均值。随着我们继续采样，我们会注意到平均值的分布正在慢慢形成正态分布。